IBRICS
Imitating Human Behaviors by Robotic Systems through Computer Vision and Machine Learning
Abstract
The research project focuses on developing a system that combines Computer Vision, Machine Learning, and Optimization-based Control for analyzing and recognizing human behaviors in realistic environments, and transferring these behaviors to robotic systems. The aim is to create a system that enables robotic systems to imitate dynamic movements and behaviors through the processing of visual data and machine learning algorithms. The project contributes to the development of intelligent robotic agents that can interact effectively both with each other and with humans in real-world situations.
The project advances innovative technologies in four main directions: extraction of human body pose from images, analysis of 3D human motion, tracking of dynamic trajectories in 3D, and development of controllers for robot manipulation. The project leverages deep learning, reinforcement learning, and optimization-based control techniques, with the goal of developing robotic systems for industrial and other applications, such as human-robot collaboration.
The project is funded by Archimedes RC: it falls under the project MIS 5154714 of the National Recovery and Resilience Plan Greece 2.0 funded by the European Union under the NextGenerationEU Program.
Publications
2. AHMP: Agile Humanoid Motion Planning With Contact Sequence Discovery. Tsikelis, I., Tsiatsianas, E., Kiourt, C., Ivaldi, S., Chatzilygeroudis, K., Hoffman, E.M. 2025. IEEE-RAS 24th International Conference on Humanoid Robots (Humanoids).
Abstract: Planning agile whole-body motions for legged and humanoid robots is a fundamental requirement for enabling dynamic tasks such as running, jumping, and fast reactive maneuvers. In this work, we present AHMP, a multi-contact motion planning framework based on bi-level optimization that integrates a contact sequence discovery technique, using the Mixed-Distribution Cross-Entropy Method (CEM-MD), and an efficient trajectory optimization scheme, which parameterizes the robot’s poses and motions in the tangent space of SE(3). AHMP permits the automatic generation of feasible contact configurations, with associated whole-body dynamic transitions. We validate our approach on a set of challenging agile motion planning tasks for humanoid robots, demonstrating that contact sequence discovery combined with tangent space parameterization leads to highly dynamic motion plans while remaining computationally efficient.
Key Contributions
- Bi-Level Optimization Framework: Integration of contact sequence discovery (CEM-MD) with SE(3) tangent-space trajectory optimization for agile whole-body motion planning.
- Automatic Contact Discovery: Eliminates the need for manual contact sequence specification through black-box optimization of contact timings and locations.
- Efficient Implementation: Generates feasible multi-contact motions in median time of ~200 seconds by leveraging parallel evaluation and SE(3) tangent-space parameterization.
- Dynamic Motion Generation: Capable of producing highly agile and dynamic whole-body motions for humanoid robots in complex environments.
Method Overview
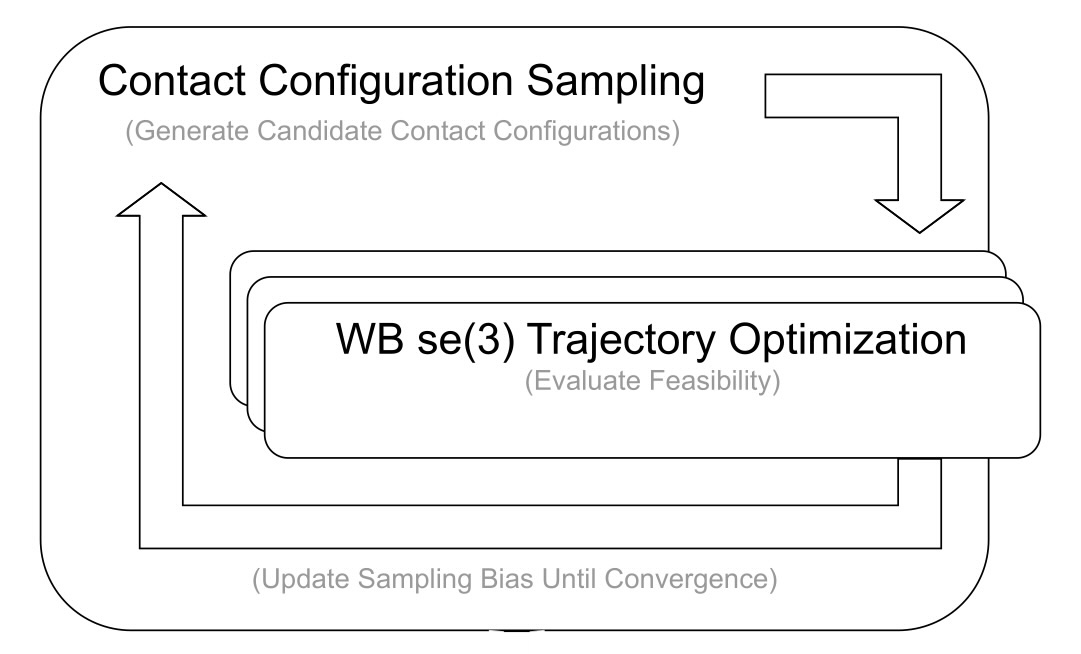
Bi-level optimization: CEM-MD samples contact sequences (outer loop), each evaluated via SE(3) tangent-space trajectory optimization (inner loop). Best solutions update the contact distribution iteratively.
Experimental Scenarios
Handrail Corridor
Move 3m forward in a handrail-equipped environment. The robot leverages dynamics for agile movements including hand-walking.
Chimney - Low Target (1m)
Climb 1m height in chimney environment. Robot weaves left-right using feet and hands to propel upward.
Chimney - High Target (3m)
Climb 3m height with more deliberate, altitude-gaining motions. Demonstrates complex contact sequences.
Experimental Results
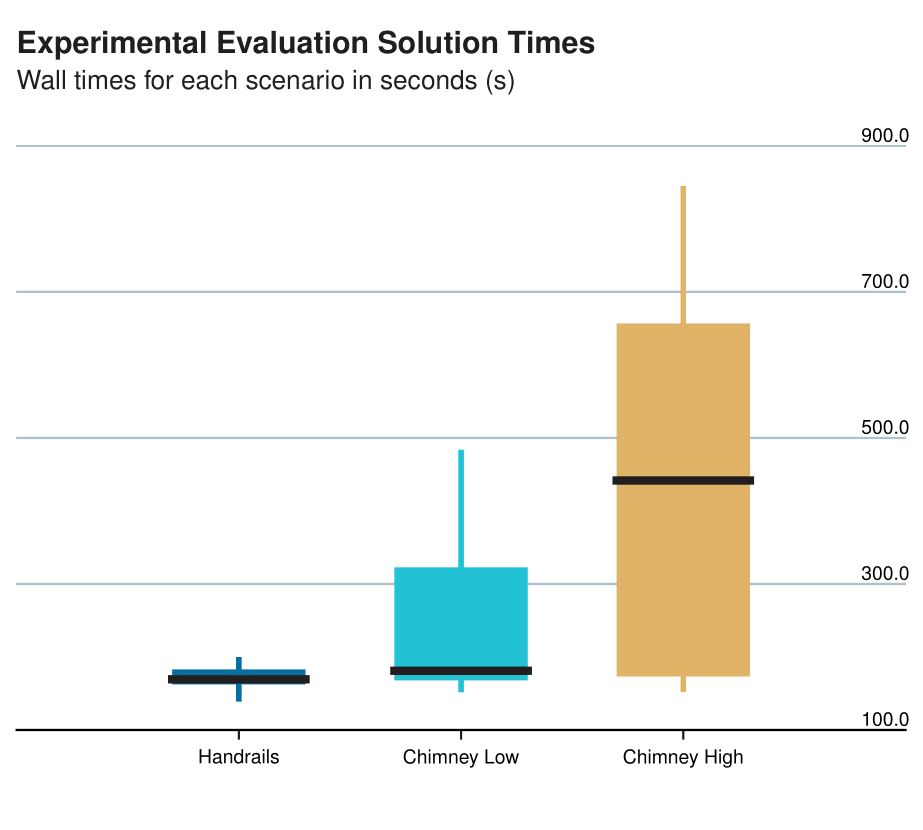
Performance Summary:
- Handrails: 100% success rate, median time ~100s (over 10 runs)
- Chimney (1m): 80% success rate, median time ~150s (over 10 runs)
- Chimney (3m): 50% success rate, median time ~300s (over 10 runs)
1. A Comparative Study of Floating-Base Space Parameterizations for Agile Whole-Body Motion Planning. Tsiatsianas, E., Kiourt, C., Chatzilygeroudis, K. 2025. IEEE-RAS 24th International Conference on Humanoid Robots (Humanoids).
Abstract: Automatically generating agile whole-body motions for legged and humanoid robots remains a fundamental challenge in robotics. While numerous trajectory optimization approaches have been proposed, there is no clear guideline on how the choice of floating-base space parameterization affects performance, especially for agile behaviors involving complex contact dynamics. In this paper, we present a comparative study of different parameterizations for direct transcription-based trajectory optimization of agile motions in legged systems. We systematically evaluate several common choices under identical optimization settings to ensure a fair comparison. Furthermore, we introduce a novel formulation based on the tangent space of SE(3) for representing the robot’s floating-base pose, which, to our knowledge, has not received attention from the literature. This approach enables the use of mature off-the-shelf numerical solvers without requiring specialized manifold optimization techniques. We hope that our experiments and analysis will provide meaningful insights for selecting the appropriate floating-based representation for agile whole-body motion generation.
Key Contributions
- Comparative Study: Systematic comparison of floating-base space parameterizations for direct transcription-based trajectory optimization in legged and humanoid robots.
- Fair Evaluation: Identical optimization/numerical settings for fairness.
- Novel SE(3) Tangent TO Formulation: New trajectory optimization formulation using the tangent space of SE(3), leveraging standard solvers without specialized manifold optimization.
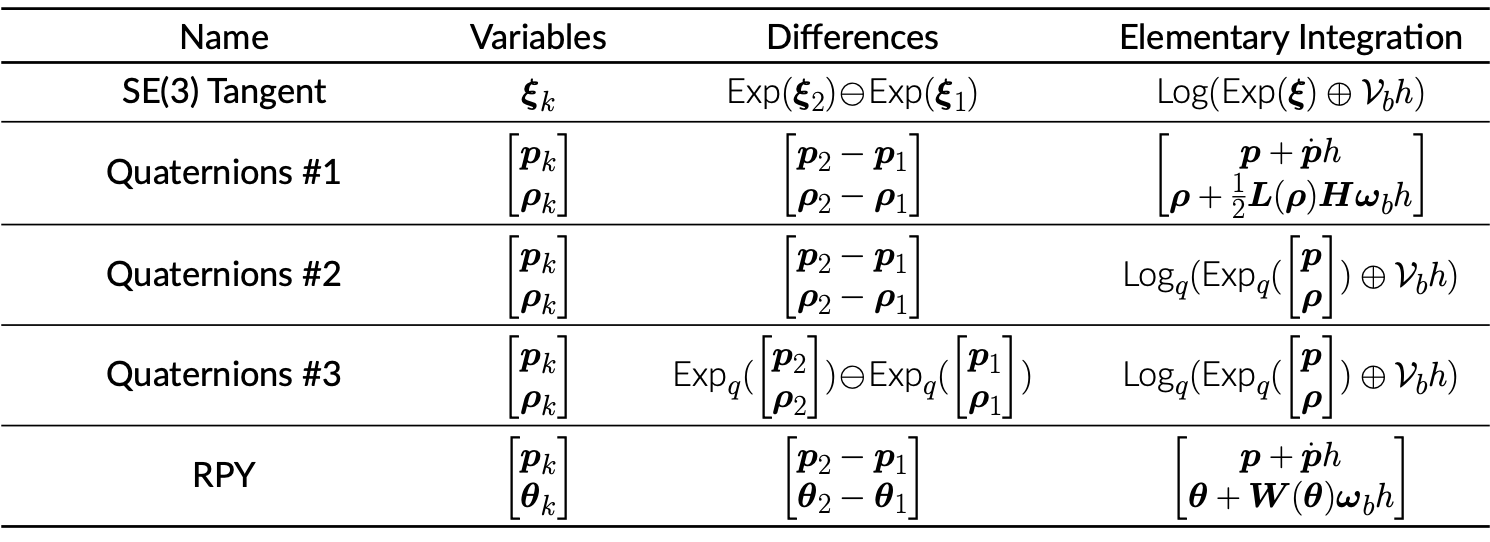
Floating-base representations compared:
Experimental Scenarios
Walk (Talos)
Straight gait, 2 m forward
Hopscotch (Talos)
Alternating double hops, 2 m course
Big Jump (Talos)
1 m forward jump
Handstand (Talos)
Stand → handstand → return
Back-flip (G1)
Somersault, 0.5 m backward
Side-flip (Go2)
Lateral somersault, 0.3 m sideways.
Experimental Results and Conclusions
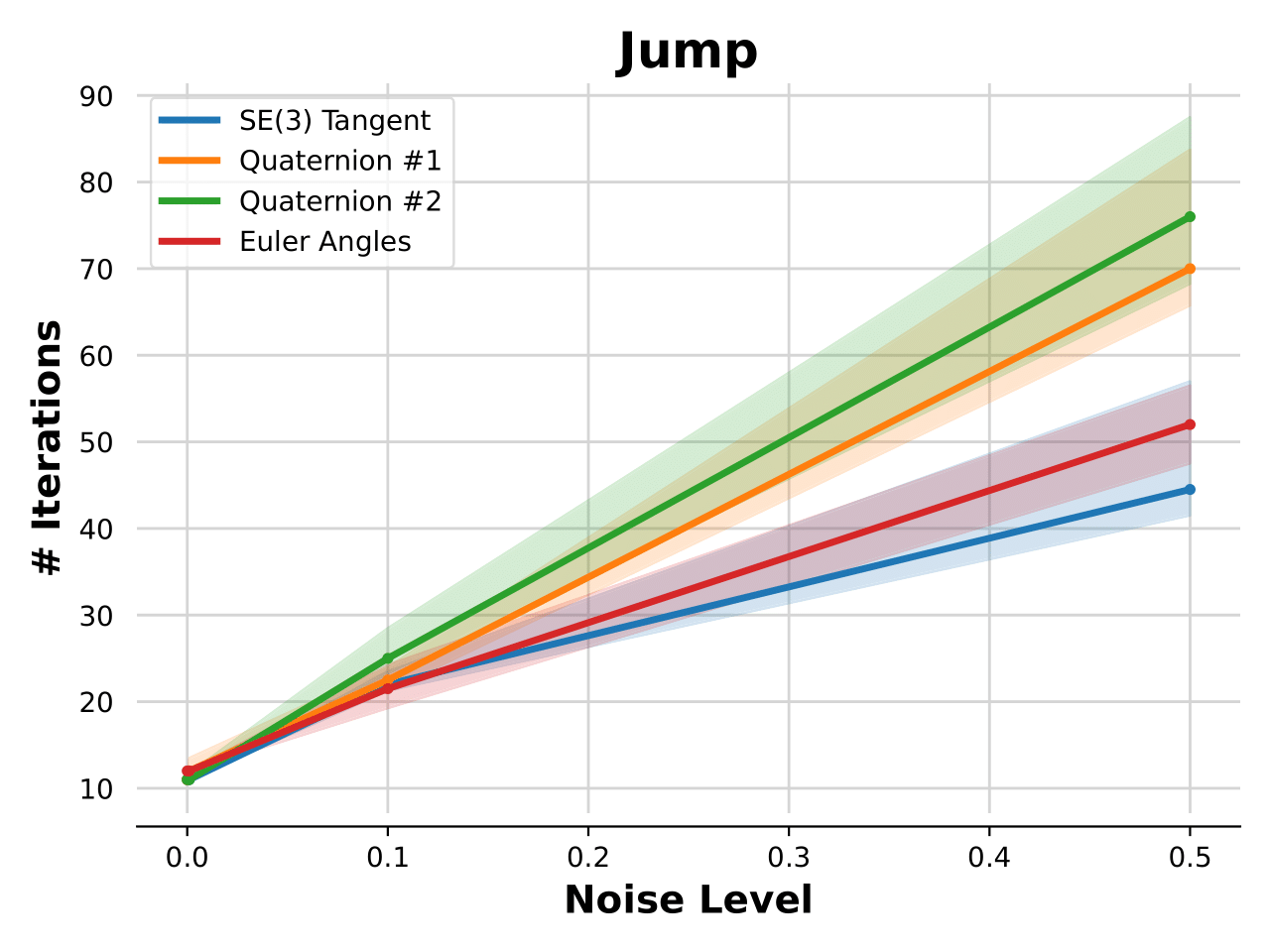
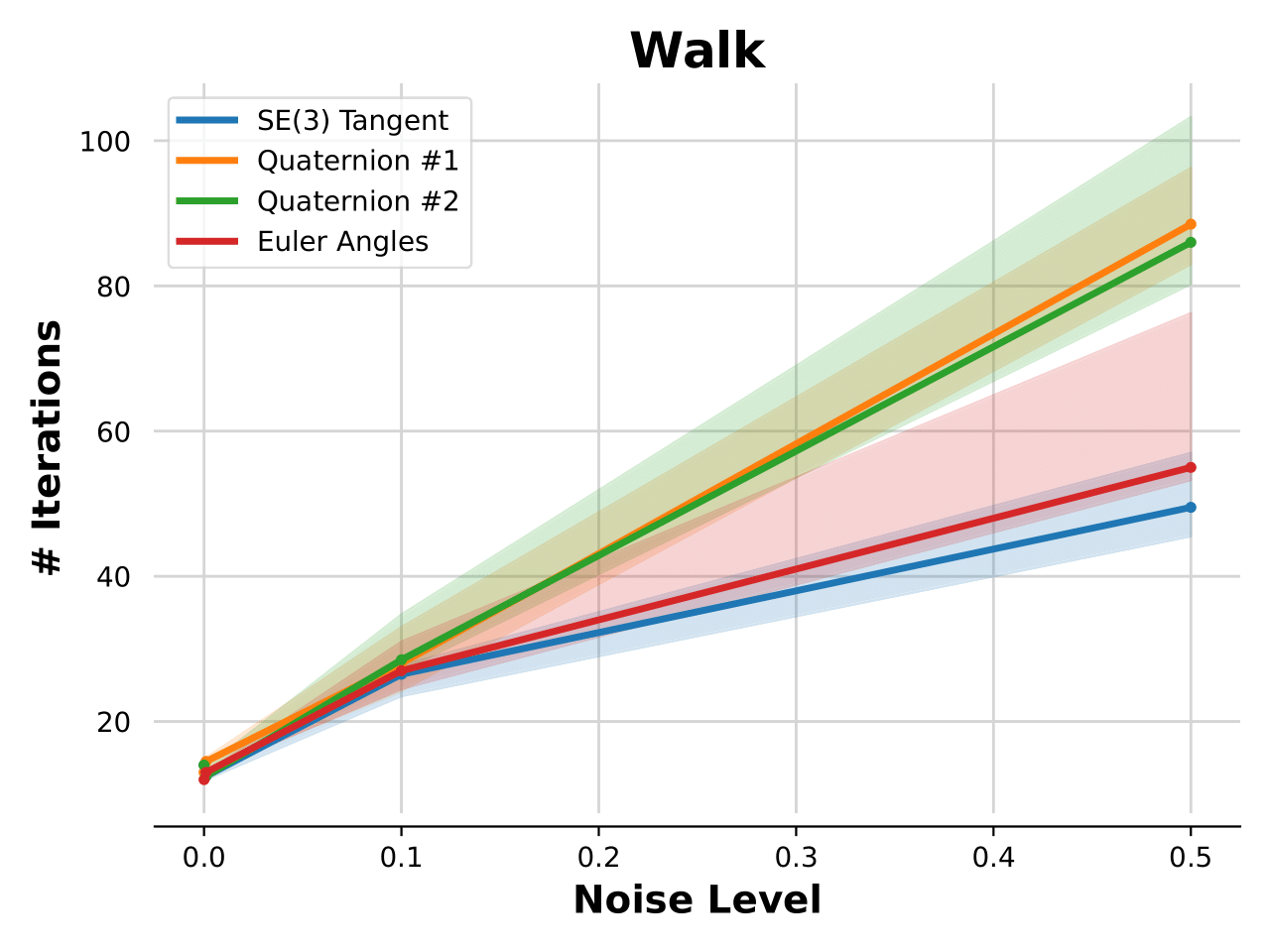
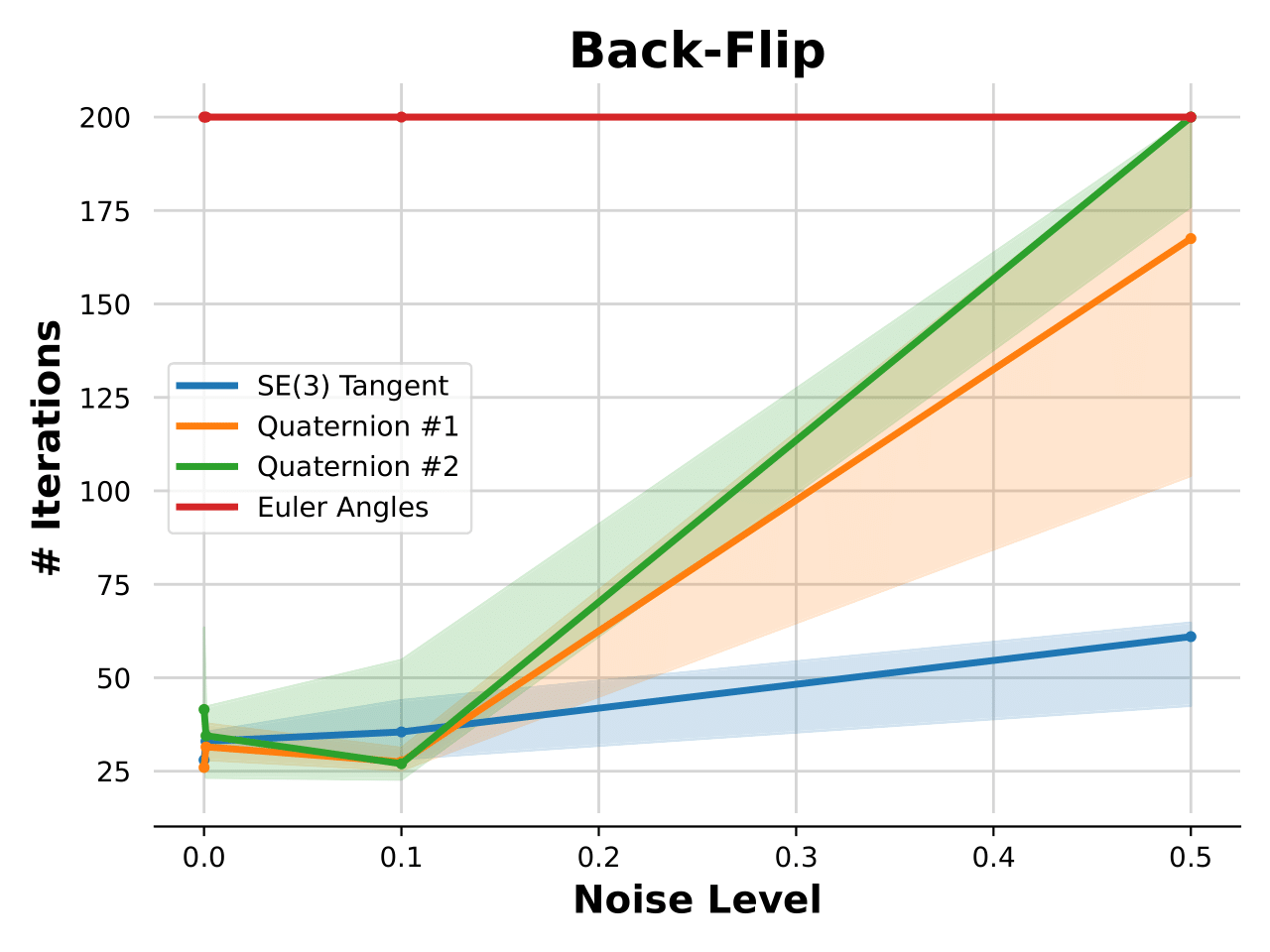
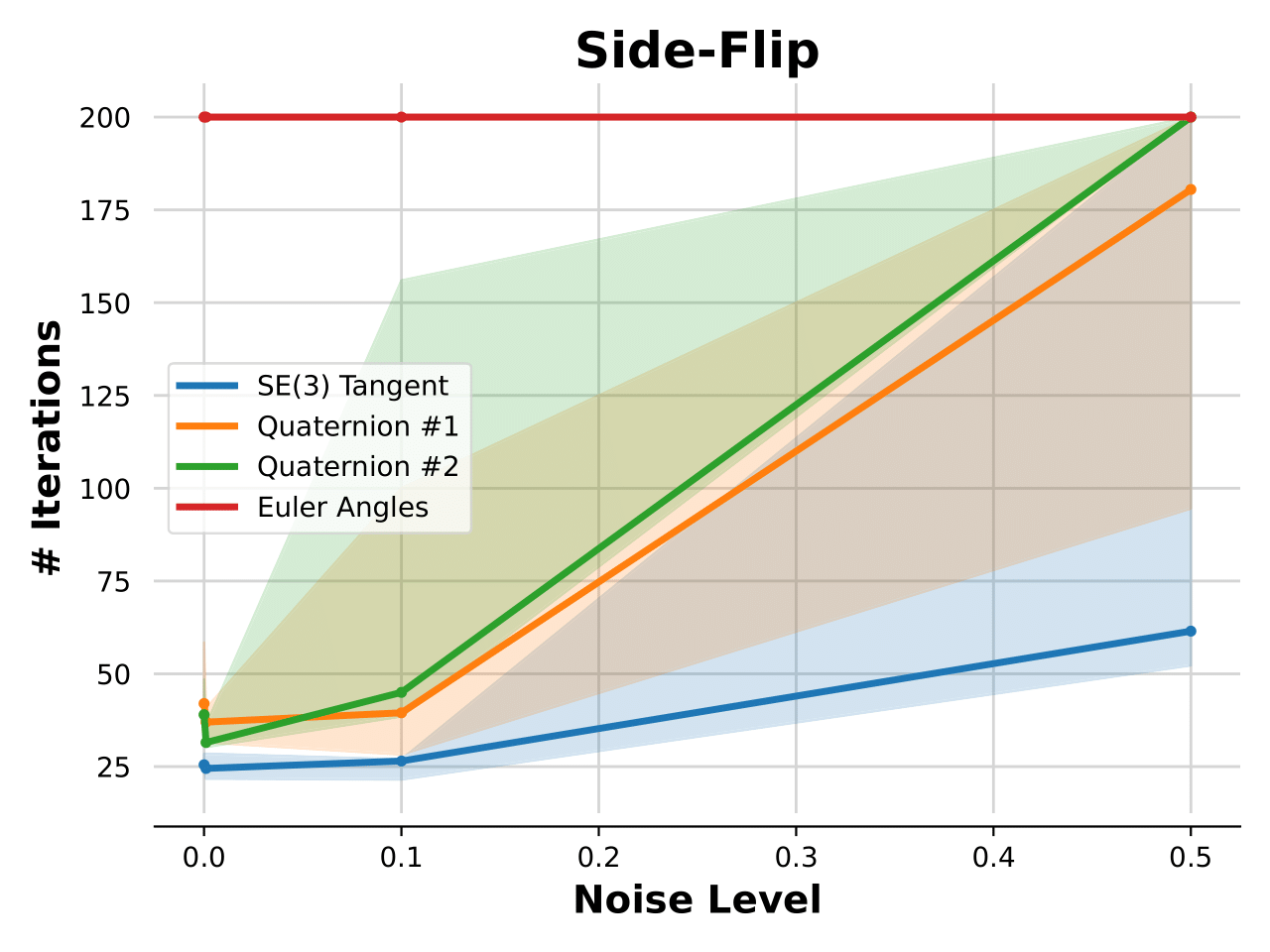
- Euler: Effective for simple tasks but fails with large rotations.
- Quaternions: Sometimes successful, but fragile; hybrids underperform.
- SE(3) Tangent: Most consistent, robust, and effective across scenarios.










